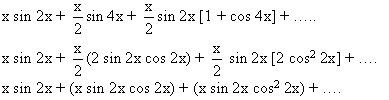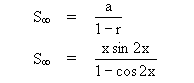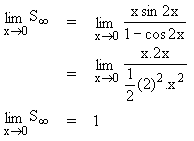|
|
Penyelesaian :
Akar-akar persamaan lama : x1 dan x2
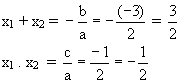
Akar-akar persamaan baru : xA dan xB
xA = 2x1 - 1
xB = 2x2 - 1
xA + xB = (2x1 - 1) + (2x2 - 1)
= 2 (x1 + x2) - 2
= 2 (
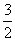 ) - 2
) - 2= 3 - 2
xA + xB = 1
xA . xB = (2x1 - 1) (2x2 - 1)
= 4 x1.x2 - 2(x1 + x2) + 1
= 4.(-
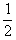 ) - 2(
) - 2(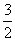 ) + 1
) + 1= -2 - 3 + 1
xA . xB = -4
Jadi persamaan kuadrat baru : x² - (xA + xB)x + xA . xB = 0
x² - x - 4 = 0
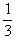
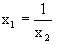
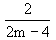 = 1
= 1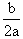
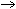 a + b + c = -4
a + b + c = -4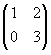 , B =
, B = 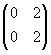 dan C =
dan C = 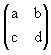 . Jika XT menyatakan transpose dari matriks X, dan C = ((A - B)T)4 , maka a + b + c - d = ........
. Jika XT menyatakan transpose dari matriks X, dan C = ((A - B)T)4 , maka a + b + c - d = ........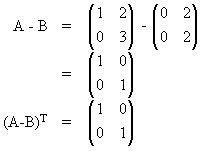
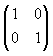
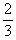
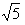
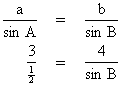
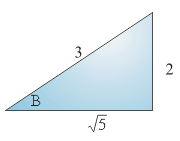
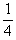
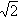
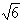
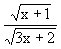 , maka tan 2B = ........
, maka tan 2B = ........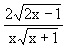
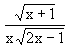
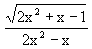
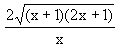
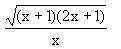
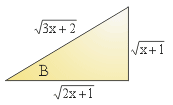
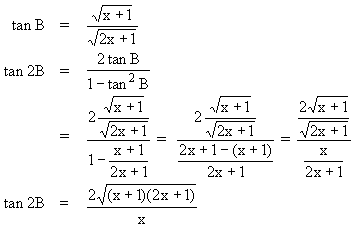
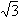 sin x + (
sin x + (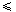 x
x 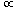 ).
).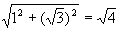 = 2
= 2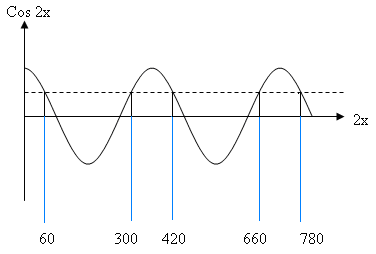
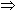 30
30 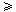 90°
90°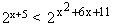 adalah ........
adalah ........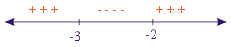
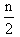 (2n + 6).
(2n + 6). 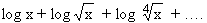 mempunyai jumlah sama dengan ........
mempunyai jumlah sama dengan ........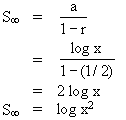
 g(x) = x³ - 2x + 1 dan g(x) = 2x + 1. Maka nilai dari f(1) adalah ........
g(x) = x³ - 2x + 1 dan g(x) = 2x + 1. Maka nilai dari f(1) adalah ........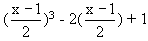
 ) dari f(x) =
) dari f(x) = 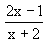 adalah ........
adalah ........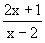 , x
, x 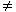 2
2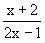 , x
, x 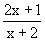 , x
, x 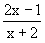 , x
, x 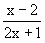 , x
, x 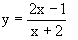
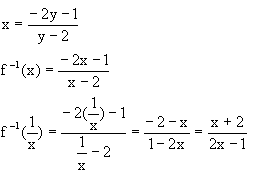
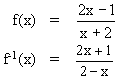
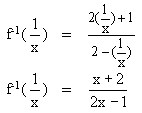
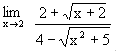 = ........
= ........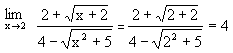
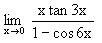 = ........
= ........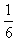
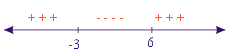
 x² + 6x - 1 dalam interval -2
x² + 6x - 1 dalam interval -2 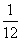
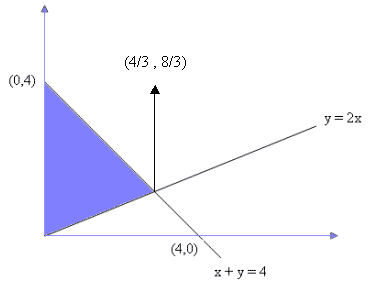
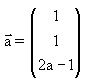 dan
dan 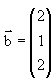 . Agar panjang proyeksi vektor a pada b adalah 2, maka nilai a = ........
. Agar panjang proyeksi vektor a pada b adalah 2, maka nilai a = ........
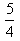
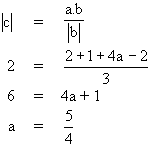
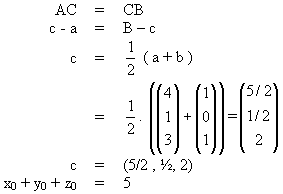
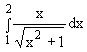 = ........
= ........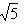
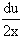
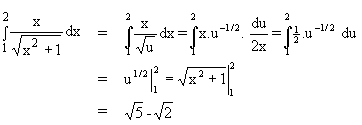
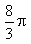
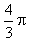

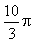
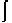 x² dy
x² dy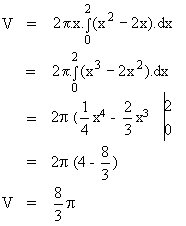
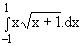 = ........
= ........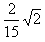
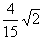
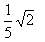
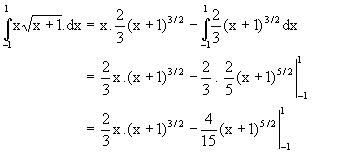
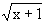 , maka F'(x) = ........
, maka F'(x) = ........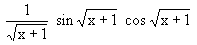
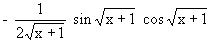
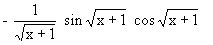
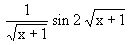
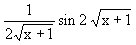
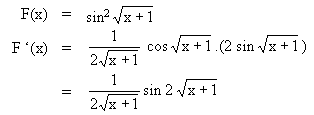
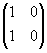 menghasilkan bayangan ........
menghasilkan bayangan ........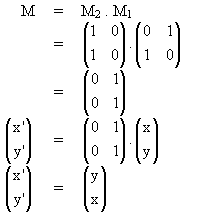
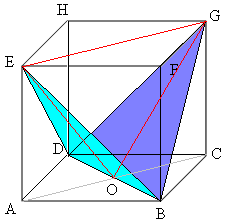
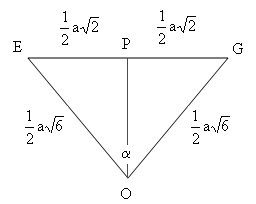
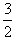 a² +
a² + 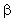 adalah sudut yang dibentuk bidang TAD dan alas limas, maka tan
adalah sudut yang dibentuk bidang TAD dan alas limas, maka tan 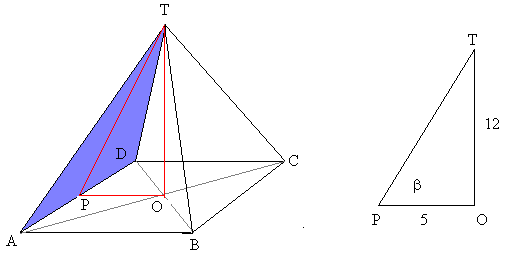
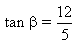
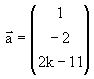 akan tegak lurus pada vektor
akan tegak lurus pada vektor 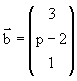 jika p = ........
jika p = ........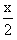 sin 4x +
sin 4x + 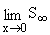 = ……..
= ……..